Item Response Theory Models for Difference-in-Difference Estimates (and Whether They Are Worth the Trouble)
When randomized control trials are not possible, quasi-experimental methods like Regression Discontinuity and Difference-in-Difference (DiD) often represent the best alternatives for high quality evaluation. Researchers using such methods frequently conduct exhaustive robustness checks to make sure the assumptions of the model are met, and that results aren’t sensitive to specific choices made in the analysis process. However, often there is less thought applied to how the outcomes for many quasi-experimental studies are created. For example, in studies that rely on survey data, scores may be created by adding up the item responses to produce total scores, or achievement tests may rely on scores produced by test vendors. In this study, several item response theory (IRT) models specific to the DiD design are presented to see if they improve on simpler scoring approaches in terms of the bias and statistical significance of impact estimates.
Why might using a simple scoring approach do harm in the quasi-experimental/DiD context?
While most researchers are aware that measurement error can impact the precision of treatment effect estimates, they may be less aware that measurement model misspecification can introduce bias into scores and, thereby, treatment effect estimates. Total/sum scores do not technically involve a measurement model, and therefore may seem almost free of assumptions. But in fact, they resemble a constrained measurement model that oftentimes makes unsupported assumptions, including that all items should be given the same weight when producing a score. For instance, on a depression survey, total scores would assume that items asking about trouble sleeping and self-harm should get the same weight in the score. Giving all items the same weight can bias scores. For example, if patterns of responses differ between treated and control groups, faulty total score assumptions could bias treatment effect estimates and mute variability in the outcome researchers wish to quantify.
What decisions involved in more sophisticated scoring approaches impact treatment estimates?
Even when one uses a more sophisticated approach than total scores, biased scores can result if the model does not match the study design. For instance, a simple IRT model (often used by test vendors) assumes that there is only one mean and variance in the population. This assumption can be consequential. Many IRT-based scoring approaches will shrink uncertain scores towards a population-level mean. If one uses an IRT model that assumes there are separate control and treatment groups, then scores will get pulled towards those group-specific means and away from each other. If one uses a simple IRT model, control and treatment means would be pulled towards some in between value, which can downwardly bias treatment effect estimates.
How much do these choices matter in the quasi-experimental/DiD context?
My study demonstrates that treatment estimates across simulated datasets for a DiD in which the true effect is .20 SDs can be downwardly biased by more than half if an inappropriate scoring approach is used. The estimates use several scoring approaches ranging from a simple IRT model that ignores group membership and differences over time, to one that has multiple groups and multiple timepoint (the bottom row also includes true scores, the person’s actual score stripped of measurement bias and error). As the figure shows, when using a model that ignores group membership (i.e., that assumes only one mean and variance in the population), the estimated treatment effect is downwardly biased by more than half (on average) and the proportion of significant results (in parentheses) drops from .19 using true scores to .10. These results are equally bad when using total scores. However, scoring decisions become less consequential for longer measures like achievement tests. Also, more complex IRT models can increase Type I errors, in some cases.
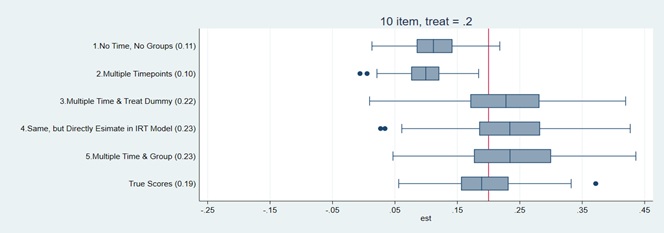
How to read this chart: This chart demonstrates that treatment estimates across simulated datasets for a DiD in which the true effect is .20 SDs can be downwardly biased by more than half if an inappropriate scoring approach (Options 1 and 2) is used.
Full Article Citation:
Soland, J. (2023). Item Response Theory Models for Difference-in-Difference Estimates (and Whether They Are Worth the Trouble). Journal of Research on Educational Effectiveness, https://doi.org/10.1080/19345747.2023.2195413.
soland_DiD_IRT_vR4.3_final.pdf
